Fraunhofer Institute for Mechanics of Materials IWMSlag sand comminution
Introduction
Slag sand is a glassy solidified granulate of blastfurnace slag, which is extracted from the liquid slag by means of fragmentation and quenching through high excess pressure water. Blastfurnace slag is ground to cement fineness and has been used worldwide for decades in the production of cement and concrete. The required fineness is set in different comminution units by separate or joint comminution with other cement constituents. The comminution energy requirement increases exponentially with the fineness. To reduce the comminution energy requirement, a more precise knowledge and improvement of the comminution-relevant properties of the slag sand is necessary. In the joint IGF project No. 20187 N, Fraunhofer IWM and FEhS - Institut für Baustoff-Forschung e.V. are investigating the influence of the porosity of slag sands on their comminution behavior.
The task
Grain models for numerical simulation with pores or cracks and hard or crystalline inclusions. The base material is shown in light blue, the bonds in orange, the hard inclusions in brown and the crystalline inclusions in dark blue.
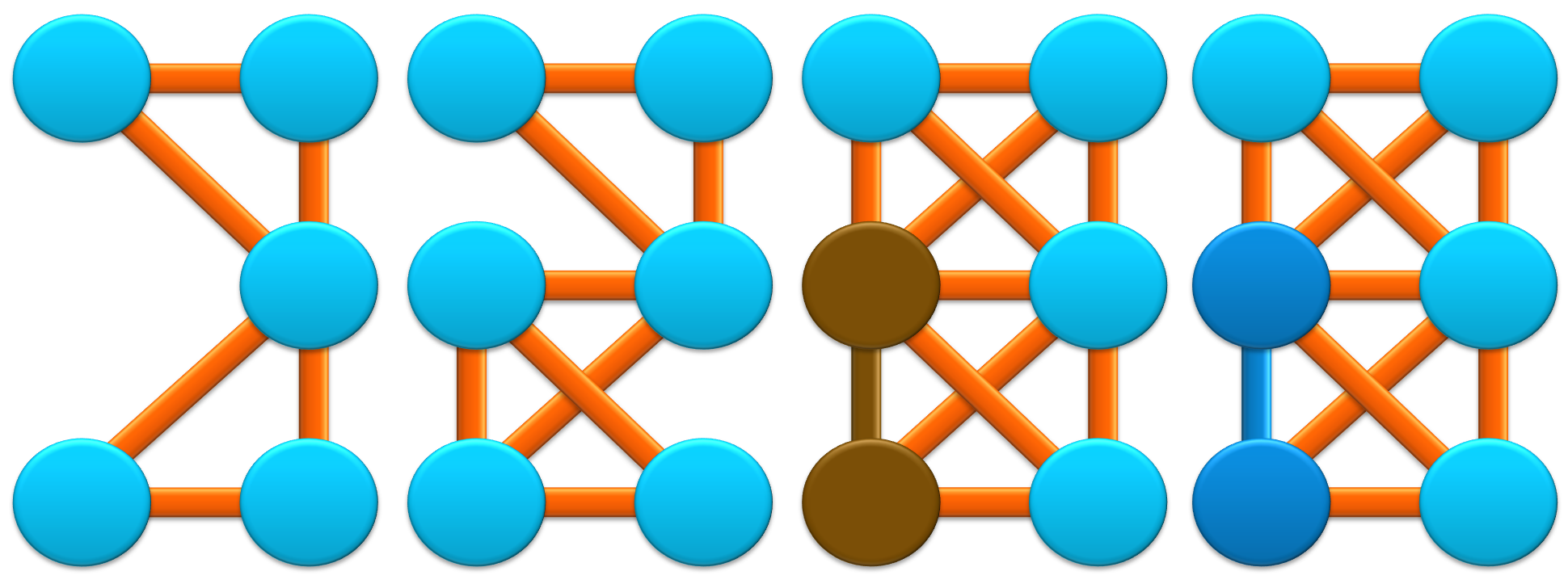
In the context of particle-based material simulation, a brittle fracture model is used to describe the comminution of the granulated blastfurnace slag. For these simulations, the representation of the grains in the form of 3D point clouds with uniform point spacing is required. First, an algorithm was implemented to procedurally create such model grains based on a set of parameters (grain volume; round or angular shape; aspect ratio; porosity; pore size). The pores are spatially randomly distributed in the grains.
In the first approach, only those model grains could be algorithmically generated which have either 100% density or a defined porosity. The pores are spherical and monodisperse. The algorithm was then extended in such a way that now also hard inclusions in the grains can be generated instead of the pores. The inclusions are again spherical and monodisperse. Thus, the influence of such inclusions on the failure behavior of the grains can also be analyzed in the numerical simulations. Instead of (infinitely) hard inclusions, it is also possible to simulate crystalline inclusions in the matrix material. For this purpose, the properties of the model including the bonds are locally varied.
In addition, an approach was developed to allow cracks in the grains to be taken into account in the modeling. For this purpose, a predetermined proportion of the internal connections (bonds), which cause the cohesion of the grain, are dissolved before the actual comminution simulation begins. This corresponds to crack damage within the grain before the comminution process. The figure next to this text shows a schematic comparison of the different models.
Results
Relative fracture toughness averaged over all load types as a function of the proportion of inhomogeneities (pores, inclusions and cracks).
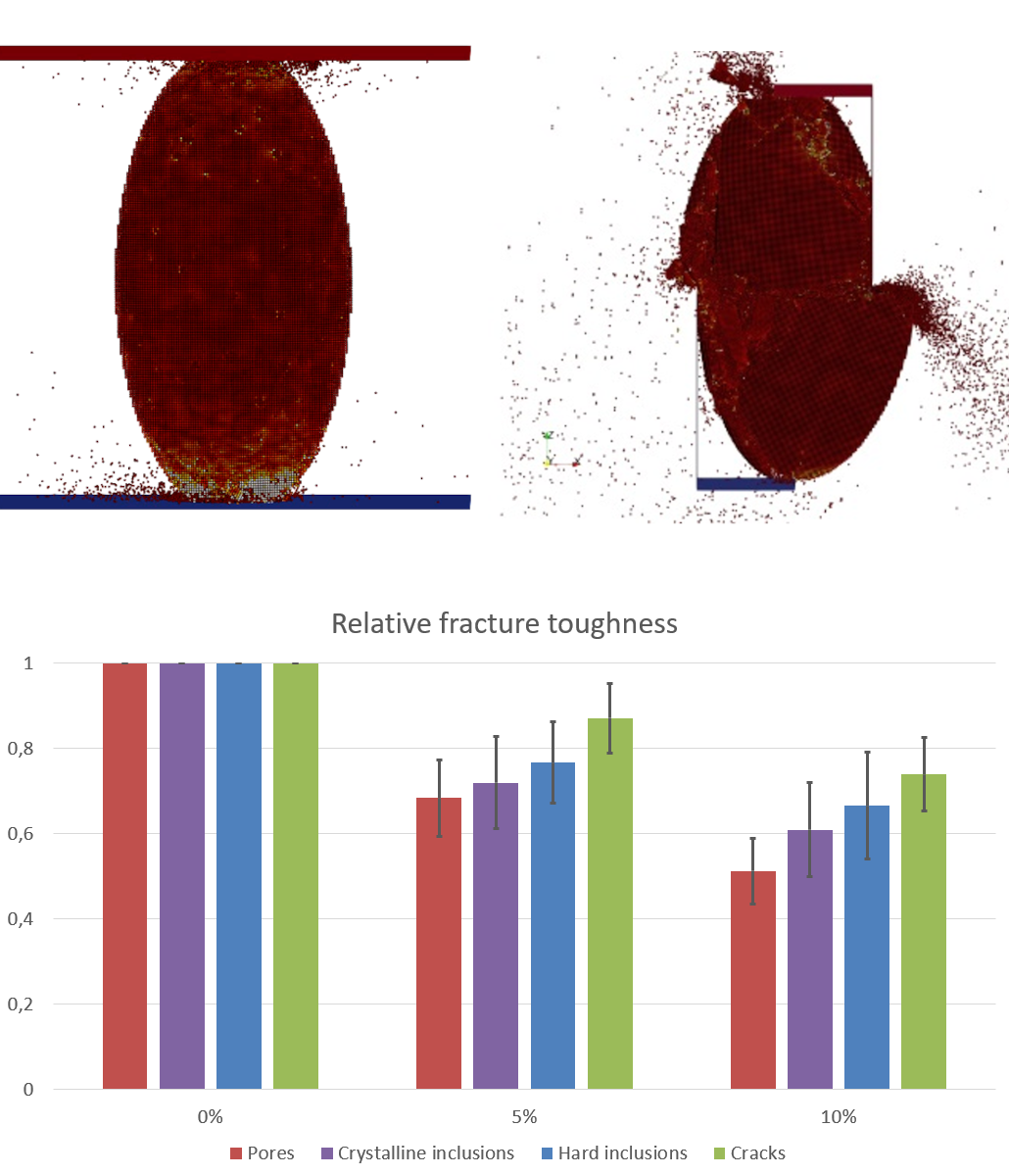
In the first part of the project, model grains in the form of spheres, ellipsoids, cubes or cuboids were loaded to failure under uniaxial compression or under shear (cf. figure). Typically, these types of loading result in the following behavior. The force acting on the grain increases linearly with the displacement path until the grain suddenly breaks. This is accompanied by an abrupt drop in the force level.
The effect that either pores and cracks or hard or crystalline inclusions have on the fracture force of the model grains was systematically evaluated across all simulations. The result is shown in the figure next to this text. The simulations show that the influence of porosity is the greatest. Already at 5% porosity, the fracture force decreases on average to 70% of the initial value. At 10% porosity, the fracture force is only half the reference value for a completely dense grain. Compared to the pores, the effect due to crystalline inclusions is somewhat smaller, followed by the influence due to hard inclusions. 10% of hard inclusions lead to about two thirds of the original breaking strength. The influence of cracks is the smallest. 10% cracks in an otherwise dense grain lead to about 70% of the reference breaking load.
According to a theoretical model by Katchanov, which argues for an increase in stress due to surface porosity, the relative fracture force should be proportional to the volume fraction within the grain, i.e., for example, at 10% porosity it should drop to 90% of the fracture force of a dense grain. However, the simulations show that the effect of porosity is much larger and nonlinear.
Snapshots from the simulation of a laboratory-scale vertical roller mill. The speed of the roller, table and slag sand is color-coded.
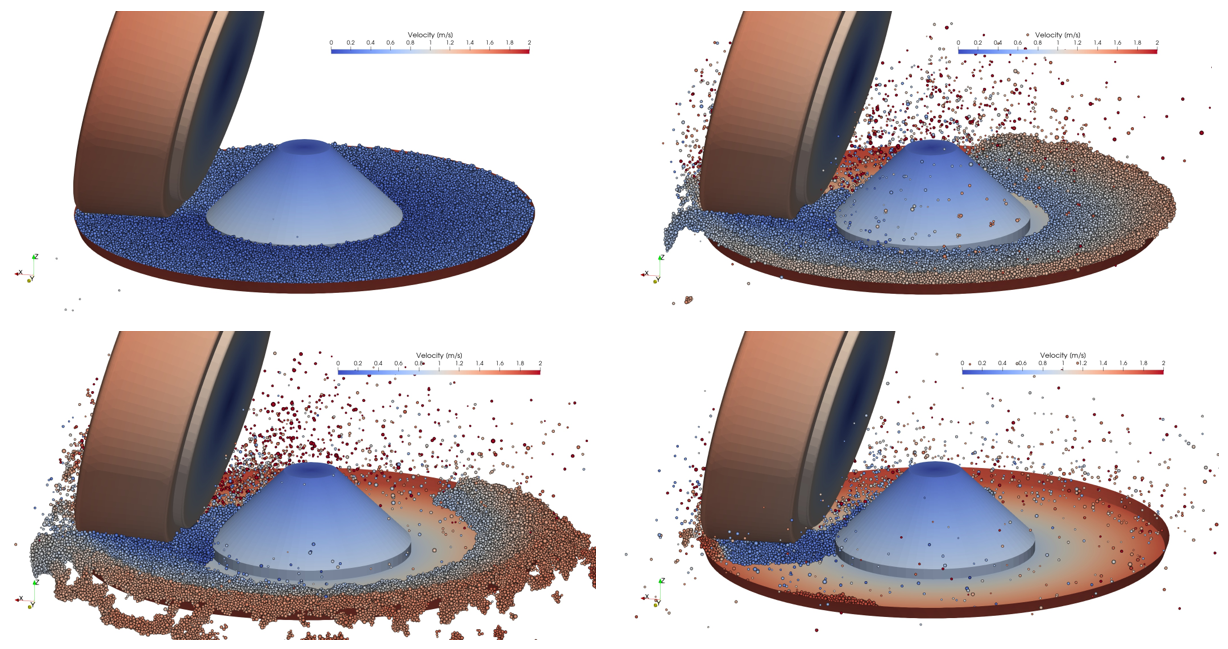
In the second part of the project, a laboratory-scale simulation model of a vertical roller mill was created in cooperation with the company Loesche. With the aid of the model of the vertical roller mill, macroscopic simulations of the loading dynamics of the slag sand in the comminution gap and microscopic simulations to determine the comminution energy were carried out. The figure shows a macroscopic simulation of the vertical roller mill. The comminution table with the initially stationary slag sand begins to rotate, causing the sand to move radially outward due to centrifugal forces. At the likewise rotating roller, the slag sand accumulates due to the narrow comminution gap. No new slag sand is fed in, but the simulation is nevertheless suitable for observations of the state in the comminution gap, since a stationary state is achieved for a short period.
Top: Simulation of the comminution of several model grains in a vertical roller mill. Bottom: Specific comminution energy as a function of the specific surface area from the simulation using grains of different porosity.
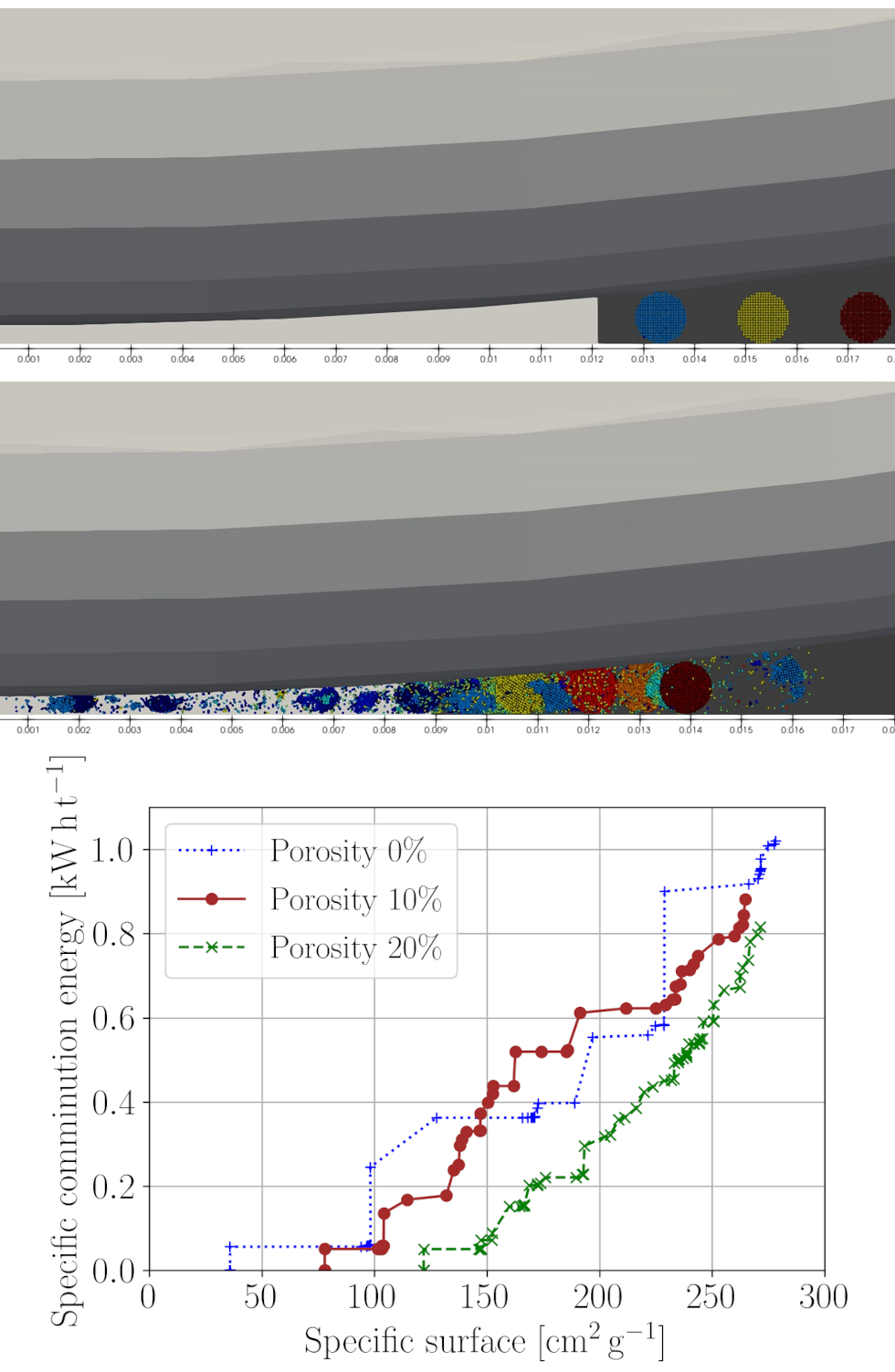
In order to be able to investigate the fragmentation behavior in the comminution gap, microscopic simulations were carried out with a few grains. These grains have a fracture model as described above. Snapshots of a simulation are shown in the figure. Here, the grains that can be distinguished by color are initially located in front of the comminution gap and are already partially fragmented in the second subfigure. The comminution gap was fixed at a certain height in these simulations. The grains are spherical with a defined porosity. The roller and the comminution table rotate at a constant angular velocity.
Analogous to the evaluation above, the specific comminution energy requirement was also plotted as a function of specific surface area for the vertical roller mill. Here, the torque acting on the roller due to the comminution of the grains was used to calculate the comminution energy. The specific surface area was again determined algorithmically by analyzing the instantaneous total surface area of the grain fragments. The result essentially shows a decreasing specific comminution energy requirement with increasing porosity for a given specific surface area. This is consistent with the result obtained for the cases of simple compression or shear showing decreasing breaking force with increasing porosity.