Fraunhofer Institute for Mechanics of Materials IWMSurface tension
Options
Surface tension is a natural phenomenon that appears every time a rain shower occurs. In technical applications the focus of interest lies particularly on the liquid-solid contact surfaces. Microfluidic devices and lab-on-chip applications for instance make use of wetting effects in order to implement valves and other means of flow control.
Technical applications often include wetting effects of complex moving geometries as well as structured surfaces. Hence, the SPH method can be well suited for simulating such problems because of its meshfree nature. For this purpose SimPARTIX® employs a recently developed and implemented state of the art wetting model that enables an accurate description of the complex multiphase contact regions based on given macroscopic contact angles and surface tensions as input parameters.
Wetting
Top: 3D-simulation of the pressure field in the cross section of drops of contact ancle 60° (left) and 120° (right) resting on a solid substrate (gray). SPH-particles are drawn as spheres whereas the pressure is interpolated on the cross section plane. Bottom: Pressure field over the symmetry axis of the drops (black line: SPH, gray points: low resolution CFD-VoF, black points: high resolution CFD-VoF).
The simulation of wetting phenomena is based on the so called continuous-surface-force model (CSF) which was originally developed for the mesh based volume-of-fluid methods (VoF) and later on translated into SPH formulations. In addition to the pure surface tension, the CSF model contains a description of the three-phase-contact (the so called triple-line) of solid, liquid and gas. This part of the original CSF model was transformed into an SPH model at the IWM and extended by a novel smoothing technique which allows a much more accurate simulation of wetting within a wide range of regimes reaching from superhydrophilic to superhydrophobic systems. Large gradients of density and viscosity are also possible.
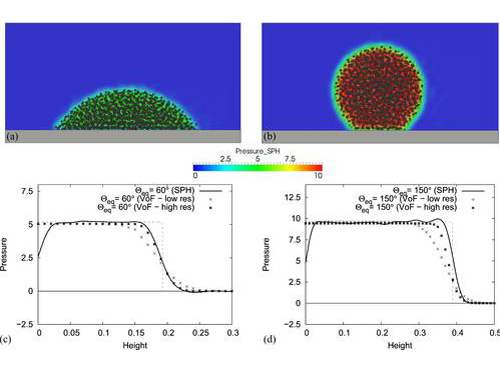
The figure below demonstrates the power of our surface tension method as implemented in SimPARTIX®. It shows an exemplary set of simulations of drops with contact angles of 60° and 120° resting on a solid substrate. The homogeneous drop shape that continues until the very end of the drop surface was validated in a parametric study for contact angles between 15° and 165°. Furthermore, we consider it remarkable that SimPARTIX® simulations produce much more accurate results than conventional CFD simulations at comparable resolution.
Structured surfaces
The pinning effect prevents drops from crossing an obstacle until the required wetting angle is met with respect to the subsequent face. (a): initial setup, (b): drops pinned at the edge, (c): drops crossed the edge.
For technical applications the wetting of structured surfaces is of particular interest, as it allows for tightly focused tailoring of the wetting conditions in different regions of a product. SimPARTIX® offers two approaches for such simulations:
highly resolved simulations of the surface structure or
simulations using effective contact angles.
With its high resolution, the first option offers a maximum of detail and is particularly suitable for design and optimization of surface structures using exemplary systems. For larger systems (e.g. an entire valve) this method would require a large number of particles and is therefore not the best choise. For such cases, SimPARTIX® offers the ability to model flat surfaces and apply effective contact angles to incorporate structured surfaces. Here, the effective contact contact angle may vary to take into account local changes of surface structures across the product.
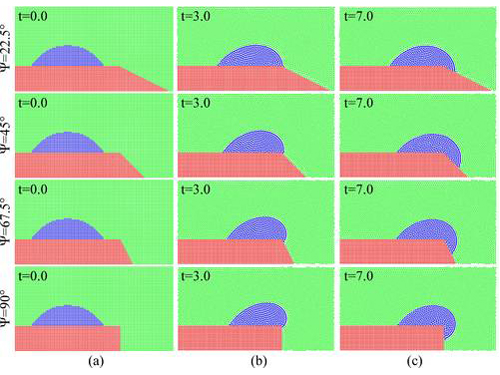
As an example for the highly resolved approach the figure below shows simulations of the so-called pinning effect which prevents drops from passing a geometrical obstacle (e.g. an edge). If we consider a drop moving towards such an obstacle (a), it will be pinned at the edge (b) and can only pass once the required contact angle is met with respect to the subsequent face (c).